Cualquier alumno de primaria, secundaria y bachillerato sabe bien que sacar un 0 o una nota cercana al 0, es sinónimo de fracaso y de suspenso, y en clase de matemáticas, ¡las notas cercanas al 0 suelen abundar!

¿Qué es el 0?
El cero (0) es uno de los números famosos de las matemáticas, y un dígito entero que simboliza el valor nulo, y para saber porqué es importante el cero, debemos saber que si se coloca a la derecha de un entero, multiplica por 10 su valor (por ejemplo: 1 / 10), mientras que, si está situado a la izquierda, no modifica su valor. ¡De ahí la expresión de «ser un 0 a la izquierda»!
Si lo usamos como cifra, con él podemos realizar operaciones como sumas, restas, multiplicaciones, entre otras. Sin embargo, al ser la expresión del valor nulo (nada, nadie, ninguno…), podemos encontrarnos con expresiones indeterminadas o que carecen de sentido, como veremos después.
En el conjunto ordenado de los enteros, el 0 es el elemento que sigue al –1 y precede al 1. Además, algunos consideran que el cero pertenece al grupo de los números naturales (los que nos permiten contar la cantidad de elementos de ciertos conjuntos), y el conjunto vacío no tiene ningún elemento.
El 0 se puede representar como cualquier número más su opuesto (o, equivalentemente, menos él mismo): X + (–X) = 0.

La ventaja de incluir el 0 en el sistema decimal posicional (el que usamos hoy en día) es que se puede escribir cualquier cifra con solo 10 dígitos diferentes (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), lo cual hace fácil operar con cantidades muy grandes. Esto contrasta, por ejemplo, con el sistema numérico romano (basado en las letras I, V, X, L, C, D y M, que, como sabes, representan los números 1, 5, 10, 50, 100, 500 y 1000). ¿Por qué? ¡Te lo explicamos!
Así, como ya sabes, en los enteros, yendo de derecha a izquierda, el primer dígito son las unidades, el segundo son las decenas, el tercero son las centenas y así sucesivamente (por ejemplo: 3874 = 3000+800+70+4). Sin embargo, en los sistemas no posicionales (como el romano) el dígito siempre tiene el mismo valor, sea cual sea su posición en la cifra.
Esto hace que se necesite una gran cantidad de símbolos para representar cantidades grandes, por lo que los hace poco prácticos para realizar operaciones con ellos (por ejemplo: en números romanos, 3874 es MMMDCCCLXXIV).
Hoy en día el 0 es un elemento fundamental en el cálculo. Por ejemplo, constituye la mitad del sistema binario (0 – 1) que se usa en la programación informática.
El cero: una historia antigua milenaria
La introducción del 0 en el sistema numérico para simbolizar la ausencia de un objeto o cantidad, no se llevó a cabo sin dudas y problemas por parte de nuestros antepasados.
Todos los alumnos aprenden el 0 en primaria, al aprender los enteros naturales y lo necesitamos para aprender los números perfectos.
Por lo tanto, parece lógico colocar el 0 tanto como un número para marcar una posición de vacío, como una cifra para expresar una cantidad nula. El 0 sirve, entre otras cosas, como marcador para delimitar los positivos de los negativos.
Pero no siempre ha sido así porque escribir lo que es nulo choca con la concepción filosófica y religiosa de las antiguas civilizaciones.
Los antiguos griegos creían que lo que existe es «uno», pero no tenían la capacidad de abstracción necesaria para poder escribir lo que no es, lo que es inexistente. Para Aristóteles, por ejemplo, el vacío y el infinito no existían. En consecuencia, los griegos no tenían un sistema de escritura que incluyera el cero en su numeración.
Después, los seléucidas babilonios (en la época de Alejandro Magno, hacia los siglos IV y III a.C.) usaron el 0 como una posición de referencia, para distinguir la nulidad entre los números. Por ejemplo, los babilonios escribían «35» y «3 5» para 305.
Utilizado por los mayas durante el primer milenio de nuestra era, el cero tenía una función posicional entre los números, pues los mayas lo utilizaban para marcar las fechas del calendario y para expresar las duraciones.
El cero: imprescindible en la historia de las matemáticas
Cuando podemos leer la historia de las mates vemos que está llena de bloqueos y descubrimientos sucesivos (como el descubrimiento del número e, por ejemplo) según la importancia de las religiones o según si los eruditos inventan herramientas poderosas para progresar en aritmética, álgebra o para elaborar un teorema.

Alrededor del siglo V, el 0 aparece como un número en sí mismo. Los hindúes, que representaban el cosmos como un universo que se extiende hasta el infinito, inventaron el cero, tal como lo conocemos hoy.
Brahmagupta, en el 628, publica Brahma Sphuta Siddhanta, un tratado sobre astronomía que define el 0 como la resta de una cifra por sí misma (x - x = 0). Ahí, los hindúes inventan la primera ecuación con resultado nulo.
Hay que decir que, para los budistas e hindúes, el concepto de la nada es fundamental para alcanzar el nirvana. La representación del cero es, por tanto, natural para ellos.
Gradualmente, los matemáticos especifican las propiedades matemáticas del número 0 tratando de sumarlo, restarlo, multiplicarlo y dividirlo, a veces en vano. En matemáticas, no podemos dividir una cifra entre cero, ya que va más allá del razonamiento matemático y es considerado un error por todas las calculadoras.
Por otro lado, al dividir el 1 entre un valor muy cercano al cero, por ejemplo, 0,01, se obtiene 100. La división de 1 entre 0,0000001 da 1 000 000. Por tanto, los hindúes descubrieron que cuanto más dividimos un dígito por un valor aproximado a 0, mayor es la distancia del resultado dígito. Entonces descubrieron que el cero está íntimamente ligado al infinito, de ahí la propiedad de que 1/x es igual al infinito.
En los países árabes, la palabra «cero» se dice con la palabra sifr, una etimología que también dará en español la palabra «cifra». ¿Lo sabías?
El 0 aparece en el siglo XII en Europa a través de la lengua árabe, hablada en la España musulmana, gracias a las sucesivas herencias de los matemáticos árabes.
La palabra sifr, importada por Leonardo Fibonacci (1175-1250), se introduce en todos los países europeos y se traduce al latín como «zephirum», que gradualmente se convierte en «zephiro», «zeuero» y finalmente «cero» en español, «zero» en italiano y «zéro» en francés.
El sistema decimal enriquece y facilita el comercio internacional. De este modo, los comerciantes contribuyen a imponer el 0 en la numeración, aunque los líderes cristianos prohibieran el uso del 0, que representa la nada, la encarnación del Diablo.
En 1202, Leonardo F, que había viajado por África, Oriente Medio, Grecia y Egipto, publicó Liber abaci, un libro aritmético que compila todo el conocimiento matemático que se conocía en el mundo de la época, antes de la aparición del número i.

La aparición del símbolo
La primera vez que aparece la simbolización «0» tal y como la conocemos en la actualidad es en el siglo IX y aparece en una inscripción en piedra, que indica el 876.
En esta inscripción, podemos leer que en la ciudad de Gwalior (en la India) «se plantaron unos jardines de 187 por 270 hastas (medida india), con los que podrían producir suficientes flores como para dar 50 guirnaldas al día a los empleados del templo Chaturbhuj».
Los dos ceros que aparecen en el 270 y el 50 están escritos casi como lo haríamos hoy en día, solo que el 0 es algo más pequeño y está un poco elevado, casi como un superíndice.
No obstante, no podemos afirmar que el origen del cero fuera indio (en la India) solamente por esta inscripción, ya que el mundo árabe, el europeo y el asiático tenían mucho contacto comercial ya en el siglo IX y la inscripción no es lo suficientemente antigua como para demostrar que el 0 se inventó allí.
De hecho, hay una inscripción muy antigua del 683 de Camboya que contiene otra simbolización similar para el cero, según explica Amir Aczel en su libro En busca del cero.
Son escritos previos, como los de Aryabhata y Brahmagupta, como hemos dicho, los que apuntan a que los indios dieron su origen.
En esta línea, es importante destacar el texto matemático indio más antiguo, el manuscrito Bakhshali (hallado en el siglo XIX) que incluye una gran cantidad de fragmentos escritos desde el siglo III hasta el siglo X.
En 2017, se realizó una precisa datación arqueológica con la técnica del carbono-14 que confirma que ese manuscrito contiene la simbolización para el 0 de mayor antigüedad conocida: un punto impreso en una corteza de abedul, entre los siglos III y IV.
Las ecuaciones con el cero
Tras su nacimiento, el cero siguió creciendo como concepto. En el siglo IX, Mahavira estudia las posibles ecuaciones con el 0:
- Indica que la multiplicación de un número por 0 es 0.
- Pero se equivoca en la fracción, al asegurar que si un dígito se divide por cero permanece invariable.
Posteriormente, en el siglo XII, Bhaskara II, el último de los matemáticos clásicos, afirma que una fracción con denominador 0 designa una cantidad infinita. También se conoce a Bhaskara II por proponer un procedimiento para resolver las ecuaciones polinómicas de segundo grado (ax2+bx+c=0) muy similar al que utilizaría actualmente cualquier alumno de Secundaria.
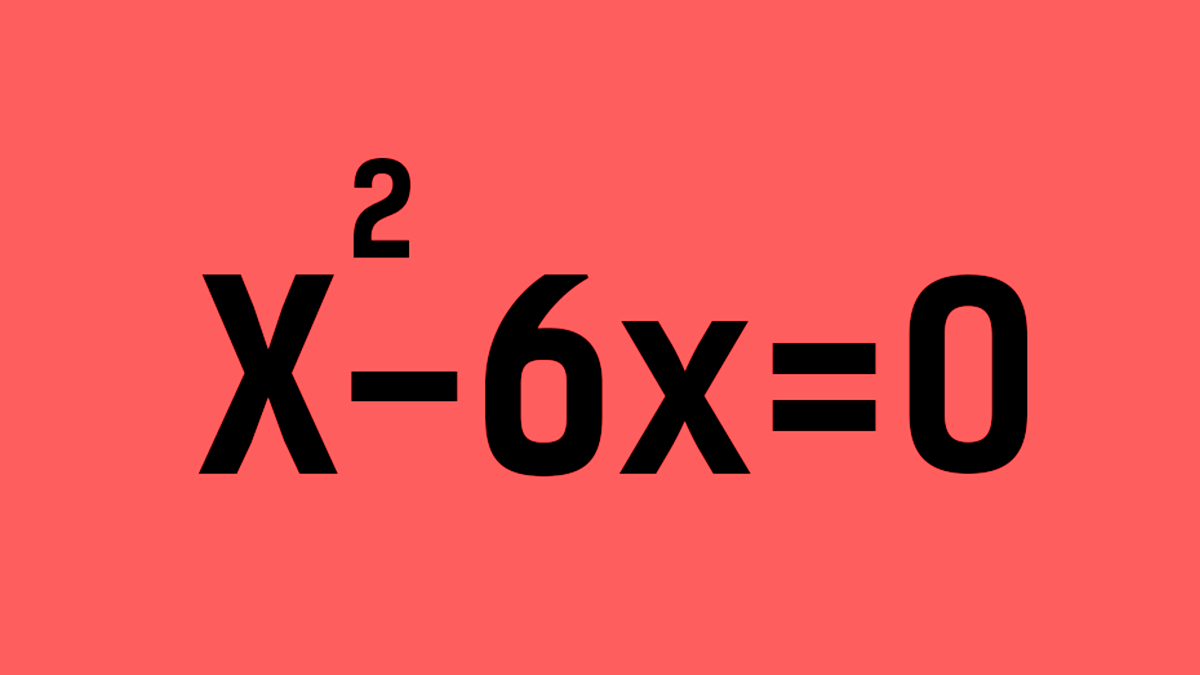
En la suma
Como sabes, en la suma el 0 es el elemento neutro. Por tanto, un número x sumado con 0 vuelve a dar x. Ejemplo: 7 + 0 = 7
En la resta
Igualmente, en la resta, el 0 es el elemento neutro. Entonces, un dígito x restado con 0 vuelve a dar x, excepto cuando el cero es el minuendo, en cuyo caso resulta -x. Ejemplos: 7 – 0 = 7 / 0 - 7 = -7
En la multiplicación
En la multiplicación, el 0 es el elemento absorbente. Es decir, cualquier cifra multiplicada por 0 da 0. Ejemplo: 7 × 0 = 0
En la división
El 0 puede ser dividido por otros números, en cuyo caso es el elemento absorbente (ejemplo: 0:7 = 0). Pero el 0 no es divisible por ninguna cifra.
En los reales, la división entre cero es una indeterminación, por lo que las expresiones 8/0 o 0/0 carecen de sentido. ¿Por qué? Pues no tiene sentido, por ejemplo, «repartir» 8 caramelos entre niños de un aula vacía, igual que tampoco tiene sentido repartir 0 billetes entre 0 personas: nada entre nadie.
Por tanto, matemáticamente, el 0 es el único número real por el cual no se puede realizar una división. Por eso el 0 es el único número real que no tiene inverso multiplicativo. Ejemplo:
- x/2 = x * 1/2 (correcto).
- x/0 = x * 1/0 (incorrecto porque 1/0 no es un número real).
En la potenciación
- Si x es distinto de 0, entonces x0 = 1
- Si n es mayor de 0, entonces 0n = 0
El valor 00 no está definido como potencia, pero según el contexto se puede elegir uno de los resultados mediante una definición. Algunas calculadoras científicas dan 1 como resultado.
En el contexto de los límites, 00 es una indeterminación, pues los límites de potencias, tales que los límites de base y exponente por separado son 0, pueden terminar dando cualquier cosa.
Paridad
En el conjunto de los enteros, podemos decir que el 0 es un par, ya que cumple con la definición de paridad y cuenta con todas las características de los pares.
Los diferentes símbolos del cero
El 0 no solo implica el punto de separación entre los enteros negativos y positivos, o la ausencia de cantidad (unidad, decenas, centenas, etc.). El 0 tiene muchos símbolos cuyo alcance no es matemático, sino filosófico, religioso o cultural.
De hecho, el 0 simboliza la nada, a veces el caos y el diablo. El 0 se usa para caracterizar el estado de lo que no vale nada, lo que es gratis (0 €, por ejemplo), infinitesimal (0,000000001, por ejemplo) o nulo.
Representa el origen de todo como punto de partida, y el alcance de los límites a alcanzar. Por lo tanto, es inseparable del símbolo del infinito (el famoso ocho acostado es un doble cero que se cierra sobre sí).
El simbolismo del 0 tiene un símbolo de unidad y eternidad, debido a su forma circular. Finalmente, representa el comienzo.
Paradójicamente, el año 0 no existe en nuestro calendario gregoriano. Del año -1 se pasa al año 1, aunque reconocemos un punto 0 de nuestra era, que se supone que corresponde al nacimiento de Jesucristo.
Aquí tienes otros significados atribuidos al cero:
- La renovación, un nuevo comienzo; ¿no decimos «empezar de 0»?
- La seguridad, por su forma redonda y cerrada.
- La fertilidad, la feminidad, el feto.
- La perfección: cada punto de la circunferencia está vinculado a su centro y equidistante.
- El ciclo, la regeneración porque el trazo del cero vuelve sobre sí.
El cero se encuentra en muchas expresiones comunes:
- Círculo de amigos (la unidad).
- Círculo vicioso.
- Empezar de 0.
- Tolerancia 0.
- Ser un 0 a la izquierda.
Expresiones con las palabras «cero» y «nulo», por lo tanto, hacen referencia tanto a significados peyorativos como meliorativos, es decir, lo bueno, lo positivo, y el estado de lo que se pierde, no existe o está ausente.
Esto es normal: simplemente en matemáticas, esta cifra es tanto positiva como negativa.
Algunas propiedades matemáticas del cero
Finalmente, ya que estamos hablando del 0 en las mates, ¿por qué no repasar algunas propiedades de esta cifra que no es tan obvia como parece?
Se dice que el 0 es un número cardinal, que representa el conjunto sin elementos. Es el entero natural más bajo, y también un elemento neutral, el único que no tiene contrario: es positivo y negativo.
Como hemos dicho, es el único valor que da un resultado sin cambios cuando se resta o cuando se suma a otro: 10 + 0; 10 - 0, 1 + 0 + 2 + 0 + 3 = 1 + 2 + 3, etc.
Historia del cero absoluto
Este proviene de una investigación que realizo William Thompson en 1848, William partió para la elaboración de este concepto de la observación de como se comportaban los gases y de como los mismos varían su volumen de forma proporcional ante el descenso de los grados °C.
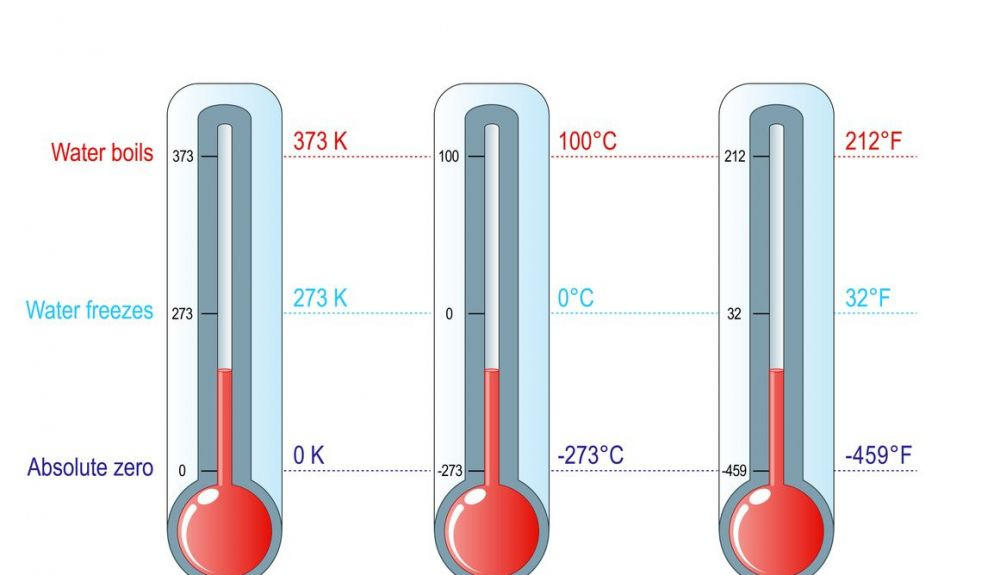
El cero absoluto es la menor temperatura posible. Corresponde, por definición según acuerdo internacional, a la temperatura de, −273,15 °C o −459,67 °F. Cuando los grados bajan a este tope, el nivel de energía interna del sistema es el más bajo posible. En otras palabras, según los preceptos de mecánica clásica, las partículas carecen de movimiento.
¡Pero el cero absoluto es un límite inalcanzable! Lo dice el tercer principio de la termodinámica (al llegar a este, cualquier proceso de un sistema físico se detiene). No obstante, se ha intentado varias veces llegar a este grado de calor, ¡y casi se ha alcanzado!
En septiembre de 2014, científicos italianos del proyecto CUORE (Cryogenic underground observatory for rare events) del Instituto Italiano de Física Nuclear enfriaron durante 15 días un recipiente de cobre de un metro cúbico y 400 kilos en un criostato hasta los 0,006 kelvins (−273.144 °C) rozando el cero absoluto y estableciendo un récord en el universo conocido sobre un volumen tan grande.
Los investigadores tardaron alrededor de diez años en diseñar y fabricar el criostato, la tarea compleja del experimento, ya que la dificultad para llegar a un grado de calor tan bajo en una cámara de enfriamiento es el hecho que las moléculas de la cámara, al llegar a este, no tienen energía suficiente para hacer que esta siga descendiendo.
Este experimento se había llevado a cabo para estudiar las propiedades de los neutrinos y otras partículas, lo cual permitiría demostrar, por primera vez, la transformación de antineutrinos a neutrinos, lo que ofrece una posible explicación para la abundancia de la materia sobre la antimateria en nuestro Universo.
¿Quieres aprender los números primos? ¿Quieres aprender el número áureo? ¿Tu hijo no sabe realizar ecuaciones simples con el 0? Hay muchas formas de dominarlas: a través de clases y ejercicios en línea, aprende el número Pi en clases particulares a domicilio con nuestros profesores de Mates en Superprof, recuerda que la primera clase es gratis.
Resumir con IA:















