«El éxito no es para los que piensan que pueden hacer algo, sino para los que lo hacen».
Euclides
La historia de las matemáticas cuenta con grandes nombres a lo largo de los siglos: Pitágoras, Tales, Newton, Arquímedes o Euclides; este último se dedicó a reunir todos los conocimientos de su tiempo en un libro denominado Elementos.
Asimismo, sentó las bases de las matemáticas tal y como las aprendemos en la actualidad. Trigonometría, razonamiento sobre la álgebra, ecuaciones, fracciones, logaritmos y demás son temas que estuvieron marcados por determinados descubrimientos de la Antigüedad.
El axioma euclidiano, la división euclidiana, la geometría euclidiana, el algoritmo de Euclides... ¿Quieres progresar descubriendo la historia de las matemáticas a través de los descubrimientos del científico?

¿Quién fue Euclides?
Al igual que la historia de sus predecesores, Pitágoras y Tales, la historia de Euclides tampoco está muy bien documentada. Solo se han encontrado determinados textos que datan de varios años después de su muerte y que permiten hacerse una ligera idea de lo que vivió este personaje.
Euclides nació en Atenas alrededor del 330 a.C. Enseñó en Egipto, en la bella ciudad de Alejandría. Durante el reinado del rey Ptolomeo I, Euclides frecuentó los pasillos del Museo, un verdadero centro intelectual de Alejandría.

A diferencia de sus predecesores, Euclides no creó una escuela de matemáticas. Sin embargo, el científico ciertamente tuvo varios estudiantes y discípulos a su lado, tanto para enseñarles todo el conocimiento que poseía, como para ayudarlo en sus experimentos.
Euclides destacó por su obra titulada Elementos, que había escrito alrededor del 300 a.C. Esta obra constituyó un gran éxito y fue posteriormente comentada y analizada por importantes científicos, entre ellos Proclo y Heath.
El conocimiento de Euclides se basó en el conocimiento ya adquirido por los grandes matemáticos de la Antigüedad. Los descubrimientos de Euclides y sus contemporáneos siguieron inspirando a la ciencia mucho después de su supuesta muerte en el año 265 a.C. en Alejandría.
El libro de matemáticas de Euclides: Elementos
Aunque escribió otras obras, Elementos, el libro principal de Euclides, contiene todas las demostraciones de conocimiento geométrico de las que el genio griego sabía. Elementos, dividida en 13 libros, se centra principalmente en la geometría plana y la aritmética.
Los primeros seis libros de Elementos tratan sobre geometría plana. Encontrarás datos sobre el triángulo, líneas paralelas, el teorema de Pitágoras, figuras planas, propiedades del círculo (y la presencia de figuras rectilíneas en un círculo), la construcción del pentágono o las proporciones entre magnitudes.
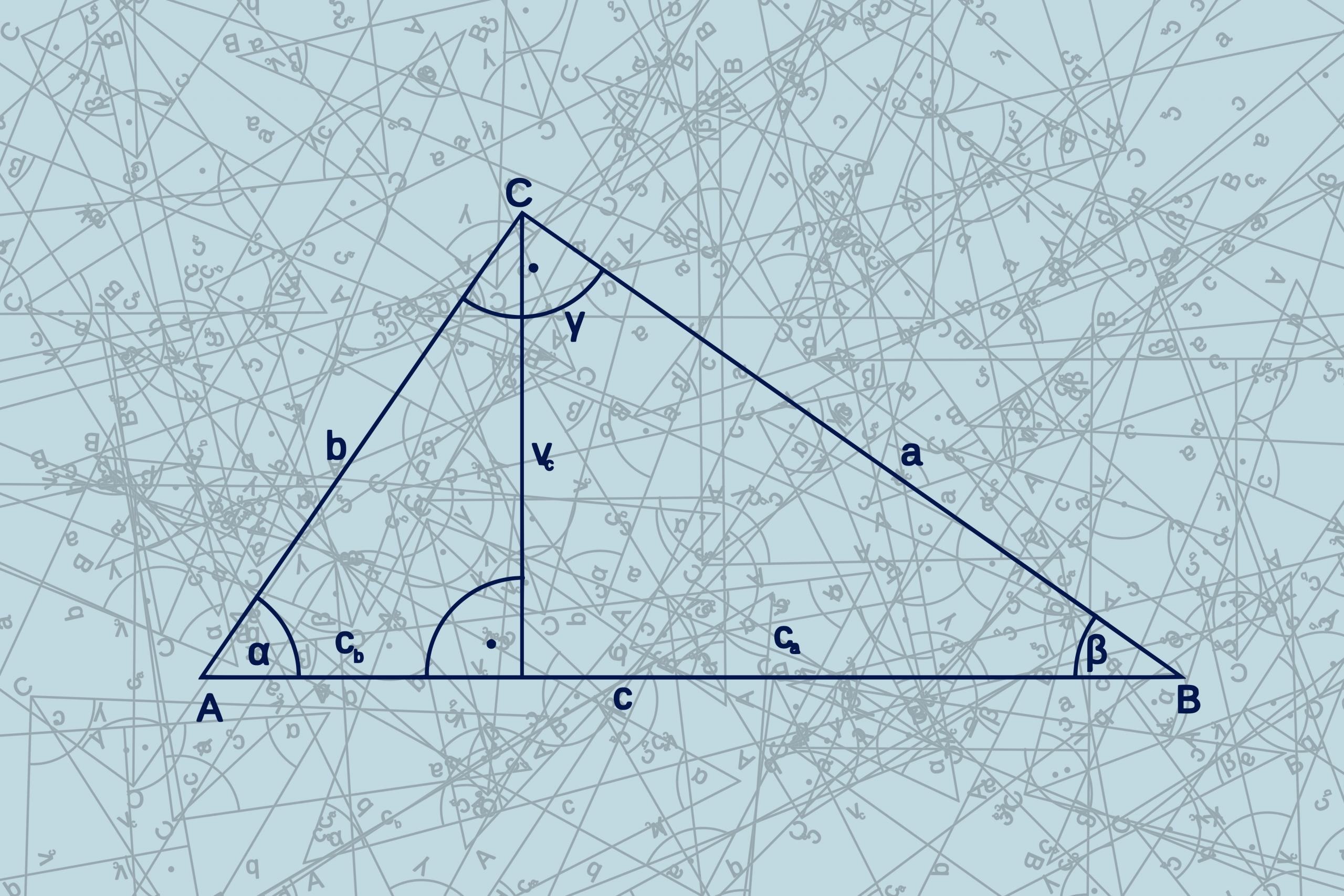
Estos primeros libros permiten establecer las bases de la geometría recordando las características de las figuras y aplicándolas mediante demostraciones.
Los siguientes tres libros ya no tratan sobre la geometría plana, sino sobre la aritmética. Euclides habló sobre números primos, la construcción del máximo común divisor de los números enteros común a dos o más enteros, números en progresión geométrica y la construcción de números perfectos.
Asimismo, en estos libros, el científico introdujo el procedimiento de las repetidas restas sucesivas, también llamadas división euclidiana.
El décimo libro se basó en las cantidades irracionales.
Los tres últimos libros están dedicados a la geometría en el espacio. Se podrá encontrar la construcción de objetos tales como la esfera, los sólidos regulares, la pirámide, el cubo, el octaedro, el dodecaedro, el icosaedro, etc.
Posteriormente, tras la edición de Euclides, se incorporaron otros libros, escritos por nuevos matemáticos que añadieron capítulos sobre poliedros regulares.
Todos los libros de Elementos sientan las bases de las matemáticas, que todavía se enseñan en la actualidad. La geometría plana o la geometría del espacio forman parte de los cursos de matemáticas que se imparten en la universidad.
Un dato curioso sobre Euclides es que fue conocido como "el padre de la geometría" por configurar la geometría en forma axiomática y constructiva.
Elementos se convirtió en una verdadera biblia de matemáticas. Durante años, muchos han considerado este libro como LA referencia del mundo matemático antes de ser cuestionado nuevamente unos pocos siglos después. Toda la información proporcionada en Elementos es una especie de fotografía de la representación del mundo físico de la época.
Si bien Elementos no aborda teoría matemática avanzada en el sentido moderno, su trabajo sentó las bases para la geometría y la deducción lógica en matemáticas.

¿En qué consiste la división euclidiana?
La división euclidiana es ciertamente una de las habilidades matemáticas que nos enseñan temprano en la escuela. Se trata de la división que nos enseñan cuando estamos en tercero o cuarto de primaria. También se conoce como división completa y está compuesta por dos enteros naturales denominados dividendo y divisor, y otros dos enteros: el cociente y el resto.

Realizar la división completa de un número A (el dividendo) entre uno B (el divisor), permite encontrar el cociente entero, es decir, el número entero que obtenemos al final de la división y el resto, es decir, la parte del dividendo que ya no se puede dividir.
Para entender esto mejor te dejamos aquí un ejemplo:
Con un dividendo de 25, dividido entre 4 (el divisor), el cociente de enteros es 6 ya que 6 x 4 = 24. Nos sobra 1. Por lo tanto, el 1 es el resto. Para hacer esto, tratamos de encontrar cuántas veces tenemos que multiplicar el divisor (el 4) para obtener el dividendo (el 25).
La representación de la división se realiza con el dividendo a la izquierda y el divisor a la derecha. El resto se sitúa por debajo del dividendo, mientras que el cociente completo aparece debajo del divisor.
Para saber si se ha terminado la división, debes estar seguro de que el resto ya no se puede dividir. Por lo tanto, debe ser más pequeño que el divisor.
Asimismo, puede ser que el resto sea cero. Entonces decimos que A es un múltiplo de B.
Aunque estos ejercicios forman parte de las clases elementales, pueden resultar complicados con decimales u otros métodos. Pero ¡no te preocupes! Basta con que recurras a nuestras clases de matematicas online para verlo todo con mayor claridad. ¡Prueba tu primera clase gratis!
Los 5 postulados de Euclides
Euclides, en su libro Elementos, nos enseña los famosos axiomas: proposiciones matemáticas que son obvias. A partir de esta definición, podemos entender que en el contexto matemático, se conoce como «axioma» a cualquier regla matemática lógica y elemental.
Euclides cita cinco en su obra:
- «Dados dos puntos se pueden trazar una recta que los une».
- «Cualquier segmento puede ser prolongado de forma continua en una recta ilimitada en la misma dirección».
- «Cualquier segmento puede ser prolongado de forma continua en una recta ilimitada en la misma dirección».
- «Todos los ángulos rectos son iguales».
- «Si una recta, al cortar a otras dos, forma los ángulos internos de un mismo lado menores que dos rectos, esas dos rectas prolongadas indefinidamente se cortan del lado en el que están los ángulos menores que dos rectos.Este postulado es conocido con el nombre de postulado de las paralelas y se enunció más tarde de esta manera: Por un punto exterior a una recta se puede trazar una única paralela».
El algoritmo de división de Euclides o el máximo común divisor
El algoritmo de Euclides también se enseña en las clases de matemáticas; seguro que te suena el famoso M.C.D. También se conoce como el máximo común denominador, que es el divisor común más grande de dos números enteros.

Para hallarlo, es necesario enumerar todos los divisores de los dos números que desees. ¿Quieres hallar el MCD de 10 y 26?
- 10: 1, 2, 5, 10.
- 26: 1, 2, 4, 9, 13.
El máximo común divisor es el número 2.
Para evitar tener que hacer la lista completa de divisores para cada número, el algoritmo de Euclides consiste en realizar una serie de divisiones euclidianas.
Por lo tanto, es suficiente dividir el número más grande entre el más pequeño y luego hacer la división hasta que se obtenga un resto igual a 0 o un resto nulo. En una división de A entre B, continuamos con una división de B entre R (el resto de la primera división), y así sucesivamente.
El algoritmo de Euclides se explica en el libro 7 de los Elementos, donde presenta por primera vez su investigación como un problema geométrico. Posteriormente, busca encontrar una unidad de medida para dos segmentos. Para ello, decide restar el segmento más pequeño al más grande y continuar hasta encontrar la medida ideal.
¡En la actualidad, este método constituye la base de cualquier división y el quebradero de cabeza de muchos estudiantes!
Si te interesa saber más de este tema, puedes buscar entre gran cantidad de videos o artículos informativos en Wikipedia (idealmente artículos con identificadores ISBN) u otros sitios en la web. ¡Sólo se trata de investigar!
Si, por otro lado, te interesa aprender de la mano de profesores particulares de matemáticas, no dudes en ingresar a nuestra plataforma. Allí podrás ver los perfiles de todos nuestros docentes, sus tarifas y las opiniones de sus estudiantes anteriores. Escoge al profesor ideal según tus gustos, ¡no te arrepentirás!
Resumir con IA:
















